TS EAMCET 2017 :: Mathematics :: General questions

• Mathematics - General questions

If the conjugate  of $(x+iy)(1-2i) $ is (1+i) , then 

Answer:

Explanation:

We have ,

 Conjugate of (x+iy)(1-2i) is 1+i

 i.e, (x-iy)(1+2i)=1+i

 $\Rightarrow$       $x-iy= \frac{1+i}{1+2i}$

 Taking conjugate both sides , we get

   $x+iy=\frac{1-i}{1-2i}$

If   $\frac{x^{2}+5}{(x^{2}+1)(x-2)}=\frac{A}{x-2}+\frac{ Bx+C}{x^{2}+1}$

 then A+B+C=

Answer:

Explanation:

We have,

$\frac{x^{2}+5}{(x^{2}+1)(x-2)}=\frac{A}{x-2}+\frac{ Bx+C}{x^{2}+1}$

 $\Rightarrow$    $x^{2}+5=A(x^{2}+1)+(Bx+C)(x-2)$

$\Rightarrow$     $x^{2}+5=Ax^{2}+A+Bx^{2}-2Bx+Cx-2C$

 Equating  the coefficient of x² ,x and constant terms , we get

 1=A+B,0=-2B+C,5=A-2C

solving these equations , we get

 $A=\frac{9}{5},B=-\frac{4}{5},C=-\frac{8}{5}$

$\therefore$ A+B+C= $\frac{9-4-8}{5}$

                   =$\frac{-3}{5}$

 For the parabola $y^{2}+6y-2x=-5$  

I. the vertex is (-2,-3)

II. the directrix is y+3=0

 Which of the following is correct?

Answer:

Explanation:

We have,

$y^{2}+6y-2x=-5$ 

 $\Rightarrow$  $y^{2}+6y=2x-5$

$\Rightarrow$   $y^{2}+6y+9=2x-5+9$

$\Rightarrow$   $(y+3)^{2}=2x+4$

$\Rightarrow$  $(y+3)^{2}=2(x+2)$

 $\therefore$   4a=2 $\Rightarrow$  a=$\frac{1}{2}$

 Vertex=(-2,-3)

  Equations of directrix

     $x+2= -\frac{1}{2}$

$\Rightarrow$   $x+\frac{5}{2}=0$

$\Rightarrow$    $2x+5=0$

Let S and S' be the foci of an ellipse and B be one end of its minor axis. If SBS'  is an isosceles right-angled triangle  then the eccentricity  of the ellipse is 

Answer:

Explanation:

 We have,

 SBS'  is an isosceless right angled triangle.

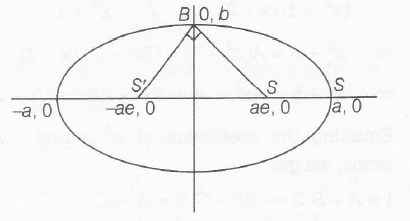
$\therefore$   $SS'^{2}=SB^{2}+S'B^{2}$

 $\Rightarrow$     $(2ae)^{2}=b^{2}+(ae)^{2}+b^{2}+(ae)^{2}$

 $\Rightarrow$   $4(ae)^{2}=2(b^{2}+(ae)^{2})$

 $\Rightarrow$   $(ae)^{2}=b^{2}$

 $\Rightarrow$   $e^{2}=\frac{b^{2}}{a^{2}}$

 $\Rightarrow$       $1-e^{2}=1- \frac{b^{2}}{a^{2}}$

 $\Rightarrow$   $1-e^{2}=e^{2}$            

                                               $\left[\because e=\sqrt{1-\frac{b^{2}}{a^{2}}}\right]$

 $\Rightarrow$          $2e^{2}=1$

 $\Rightarrow$     $e=\frac{1}{\sqrt{2}}$

A straight line makes an intercept on the Y-axis twice as long as that on X-axis and is at unit distance from the origin. Then the line is represented by the equations,

Answer:

Explanation:

Let equation of line be 

 $\frac{x}{a}+\frac{y}{2a}=1$

$\Rightarrow$ =2x+y=2a

Distance from origin is 

$|\frac{2a}{\sqrt{(2)^{2}+(1)^{2}}}|=|\frac{2a}{\sqrt{5}}|$

$\Rightarrow$   $|\frac{2a}{\sqrt{5}}|=1$

$\Rightarrow$$2a=\pm \sqrt{5}$

 Hence , equation of line is $2x+y= \pm  \sqrt{5}$

• Mathematics - General questions